Close
Bladder Wall Physics
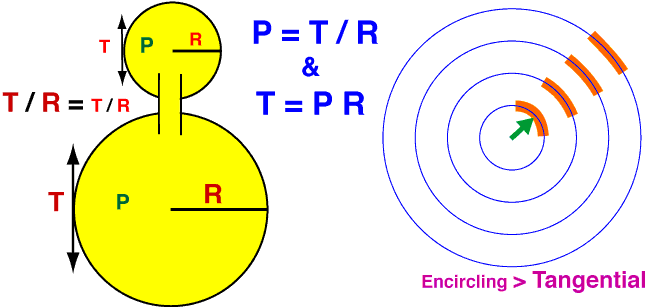
Left: The cartoon shows two spheres that have the save internal pressure (they are connected). However the wall tension (T) producing the same internal pressure (P) must be greater in the larger sphere, because T is proportional to product P*R, where R = radius.
Right: The cartoon attempts to show that a wall segment becomes less encircling and more tangential as radius expands. As volume increases, the increasingly tangential wall tension suffers a mechanical disadvantage in regard to generating internal pressure. This mechanical disadvantage explains why greater wall tension is needed to produce internal pressure as the radius expands.
In the physics of balloons & basketballs, the Law of Laplace states that lumen pressure (P) is related to wall tension (T) and container radius (R) such that: P = f * T / R, where f = 2 for a sphere. (The f value is unknown for the urinary bladder and likely to be variable and non-uniform, so it is ignored in this discussion.) The relationship, T = P * R, means that wall tension must increase to generate sufficient internal pressure for voiding when bladder volume has expanded, compared to a less-filled bladder.
Because of the T = P * R relationship, bladder wall tension is at a mechanical disadvantage in regard to generating lumen pressure when the bladder has expanded. This is so because detrusor fascicles shift from an encircling orientation toward a tangential one as the bladder enlarges. (The detrusor recovers mechanical advantage as the bladder empties during voiding.)
